Supermatma.pl

Zadanie 9:   Dwaj zawodnicy wykonują po 5 rzutów karnych. Zawodnik pierwszy strzela karnego z prawdopodobieństwem 0,8 i pudłuje z prawdopodobieństwem 0,2 ,zawodnik drugi strzela karnego z prawdopodobieństwem 0.9 i pudłuje z prawdopodobieństwem 0,1. Jakie jest prawdopodobieństwo, że zawodnik pierwszy strzeli więcej goli niż zawodnik drugi?

Rozwiązanie, strona 5:  

.

Czyli 

P(S₅>2 i T₅=2)=[0,2048+0,4096+0,32768]*0,0081= 0,00763.

P(S₅>3 i  T₅=3) = [P(S₅=4)+P(S₅=5)] * P(T₅=3):

.

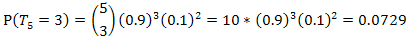Czyli

P(S₅>3 i T₅=3)=[0,4096 +0,32768]*0.0729 = 0,05375

P(S₅ >4 i  T₅=4) = P(S₅ =5) * P(T₅=4) :

.

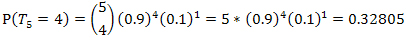 P(S₅>4 i  T₅=4) = 0,32768 * 0.32805 = 0,1075.

Zatem

P(S₅>T₅ ) = 0,00045 + 0,00763 + 0,05375 + 0,05375 + 0,1075 = 0,22308.

Odpowiedź: Prawdopodobieństwo tego, że zawodnik pierwszy strzeli więcej goli niż zawodnik drugi wynosi 0,22308.