Zadanie 3: Obliczyć pole koła wpisanego w trójkąt, którego boki tworzą ciąg arytmetyczny o różnicy równej 4.
Rozwiązanie, strona 2:
Ponieważ trójkąt ABC ma być prostokątny, zatem zachodzi w nim twierdzenie Pitagorasa. (W trójkącie prostokątnym kwadrat długości boku przeciwprostokątnej jest równy sumie kwadratów długości boków przyprostokątnych.)
Stąd
![]()
Obliczając z powyższego równania a otrzymujemy
![]()
Otrzymaliśmy równanie kwadratowe postaci
![]() zatem
zatem

Ponieważ a jest bokiem trójkąta, zatem a > 0, to
wyliczone a = -4 odrzucamy, Zatem a = 12. Ponieważ jak
obliczyliśmy wcześniej
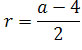 .
.
Zatem
![]()
Odpowiedź: Pole koła wpisanego w trójkąt, którego boki tworzą ciąg
arytmetyczny o różnicy równej 4 wynosi
![]() .
.