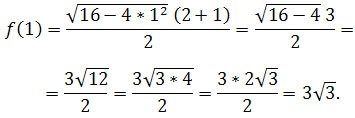Supermatma.pl
MATEMATYKA
Zadanie 8: Pole powierzchni trójkąta równoramiennego wpisanego w okrąg o promieniu R = 2 jest funkcją odległości podstawy trójkąta od środka okręgu, określić tę funkcję wzorem i wyznaczyć jej maksimum.
Rozwiązanie, strona 5:
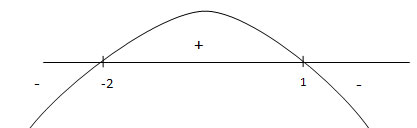
Wykresem pochodnej funkcji jest parabola
o ramionach zwróconych ku dołowi
(gdyż współczynnik przy x2 jest mniejszy od zera) i mająca punkty zerowe x1 =
1 i x2
= -2, zatem wykres znaków pochodnej jest następujący
Ponieważ funkcja
jest zawężona do przedziału x
(0 ,
2),
to punktu x2 = -2 < 0 nie bierzemy pod uwagę.
Funkcja
jest rosnąca w przedziale (0 , 1),
w punkcie x1 = 1 osiąga swoją największą wartość i
maleje w przedziale (1, 2).
Przechodząc przez punkt x1 = 1 pochodna funkcji
zmienia znak z plusa na minus, zatem warunek dostateczny istnienia ekstremum
jest w punkcie x1 = 1 spełniony i funkcja
ma w tym punkcie maksimum lokalne.
Funkcja osiąga maksimum w punkcie x1 = 1,
