Zadanie 3: Wykorzystując teorię ciągu geometrycznego obliczyć układ równań
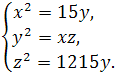
Rozwiązanie:
Wiemy, że każdy wyraz ciągu an geometrycznego z wyjątkiem pierwszego ( i ostatniego, gdy ciąg jest skończony) spełnia warunek
.Stąd, z równania
otrzymujemy, że wyrazy 15,x,y i y,x,15 tworzą ciąg geometryczny.Podobnie z równania
otrzymujemy, że wyrazy x,y,z i z,y,x tworzą ciąg geometryczny.Z równania
otrzymujemy, że wyrazy 1215,z,y i y,z,1215 tworzą ciąg geometryczny.Zauważmy, że trzy ciągi geometryczne 15,x,y i x,y,z i y,z,1215 mają ten sam iloraz, a zatem możemy z nich utworzyć ciąg geometryczny następująco 15,x,y,z,1215.
Wystarczy teraz znaleźć 3 liczby, które wstawione między liczby 15 i 1215 tworzą ciąg geometryczny.