Supermatma.pl

Zadanie 12: Obliczyć granicę .
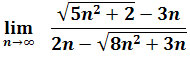Rozwiązanie:

Dzielimy licznik i mianownik przez taką potęgę zmiennej n, aby w mianowniku otrzymać wyrażenie, którego granicą jest liczba skończona różna od 0 (i którą łatwo policzymy), przeważnie jest to najwyższa potęga zmiennej n występująca w mianowniku, w naszym przypadku jest to n, zatem dzielimy licznik i mianownik rzez n, mamy

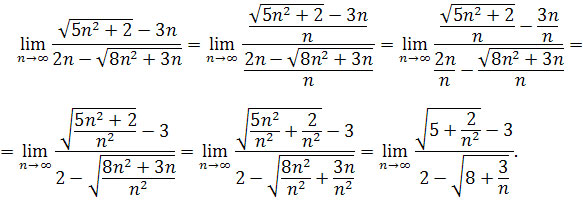
Ciągi 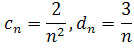są zbieżne do 0.

Zatem (na mocy twierdzenia, jeśli ciąg (a_n) ma granicę a, a ciąg (b_n) ma granicę b ( gdzie a, b są liczbami rzeczywistymi), to ciąg  (a_n + b_n) ma granicę a + b oraz  ciąg 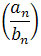 ma granicę 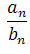) otrzymujemy