Supermatma.pl

Zadanie 2: Obliczyć granicę .
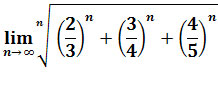Rozwiązanie:

Obliczając powyższą granicę skorzystamy z twierdzenia o trzech ciągach, czyli poszukamy dwóch ciągów, jednego ciągu o wyrazach większych od wyrazów ciągu 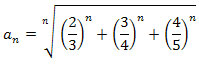 , drugiego ciągu o wyrazach mniejszych od wyrazów ciągu (a_n) i jeśli te ciągi będą zbieżne do tej samej granicy, to ciąg  (a_n) również będzie zbieżny i jego granicą będzie granica jednego ze znalezionych ciągów.

Zauważmy, że .

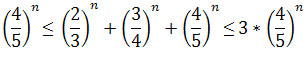Zatem 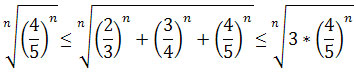, czyli

 .

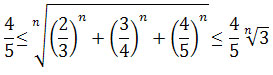Skorzystamy ze wzoru z teorii granic postaci , prawdziwego dla a > 0. Zatem i

 .

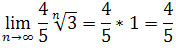Na mocy twierdzenia o trzech ciągach ciąg (a_n) jest zbieżny i jego granica jest równa 0,8.